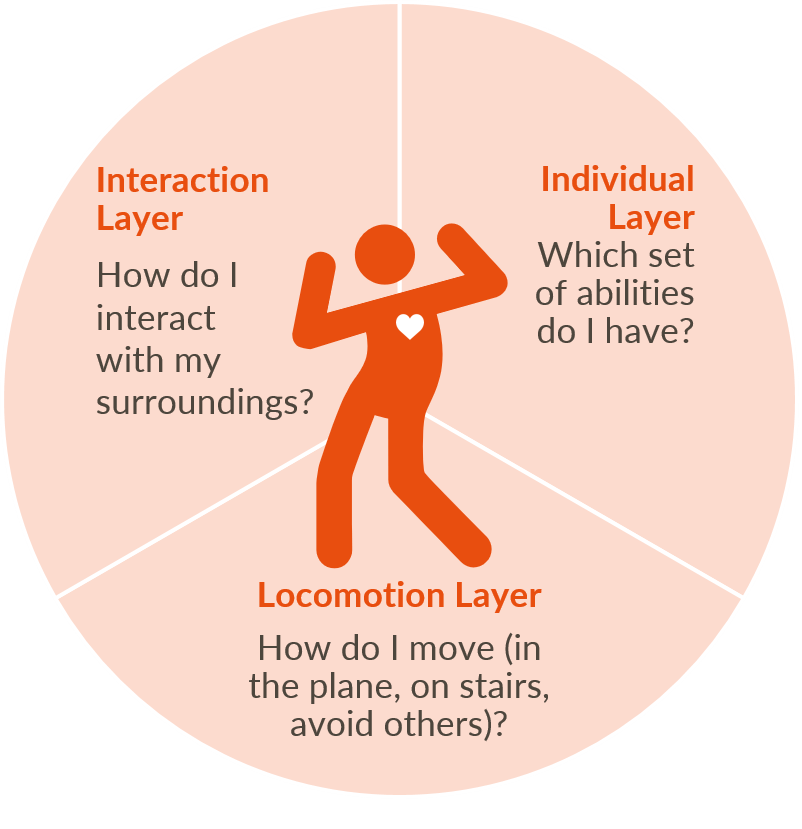
Our simulation model:
What is behind it?
The scientific model is the heart of any simulation software. The more accurately a model can reproduce real motion behavior, the more accurate the results will be. It takes four steps to get from theory to a validated simulation model.
The Optimal Steps Model breaks new ground. Instead of relying on existing models from other disciplines, it focuses on the basic tenet of crowd simulation: human movement. For this, we start with a single step. Each simulated person has a dynamic step length that depends on his walking speed and direction, and his avoidance of obstacles and other people. Thus each simulated step adjusts to current environmental conditions.
However, locomotion alone is not enough. Social psychology provides a deeper understanding of how to model human behaviour. The environment must also be included in the analysis. For this purpose, knowledge from social psychology and techniques to model behavior must be aligned. We must ask: How does a person move? What characteristics does a person possess? And how does a person interact with his environment?
Locomotion Layer
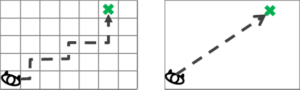
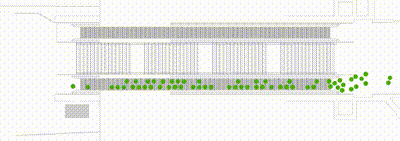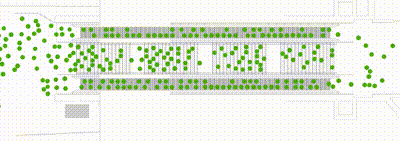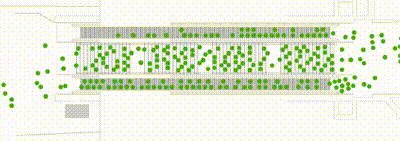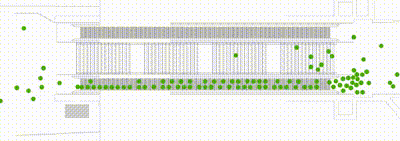
OSM: Continuous geometry: every point can be accessed
In crowd:it the locomotion layer is created as follows:
Continuous geometry
- Simulated pedestrians (agents) are free to move in any direction.
- All details of the plan are preserved. For instance, round objects can be modelled. This prevents dangerous artefacts.
Dynamic navigation field
- At each time step, agents consider which route is best under the given circumstances.
- They regard other agents as obstacles and, depending on the situation, can decide on a longer but ultimately faster route.
Optimal Steps Model
- The model imitates a real, human step.
- The underlying Optimal Steps Model facilitates implicitly realistic pedestrian behaviour. For instance, agents slow down naturally when confronted with dense crowds by taking smaller steps. This means no density-velocity relationship need be input.
Vertical connection objects
Unlike other simulators, crowd:it explicitly models stairs with their indiviual properties like the number of steps or the step depth. In other programs, for example, stairs are modelled as areas where walking speeds reduce. Due to the reduced step size on stairs, however, faster people are more likely to be decelerated more than slower people. A linear scaling is therefore not exact (cf. (10)). The stair model of crowd:it, the Optimal Stair Model, takes this knowledge into account. This means that people are also decelerated by the depth of the staircase and not exclusively depending on their speed on the level.
The Optimal Stair Model of crowd:it also reflects the insight that people tend to walk down on stairs in a straight manner and avoid slant paths on stairs. This is due to the fact that walking down stairs at an angle increases the risk of not hitting the stair step exactly and thus, in the worst case, causing a fall. In conventional models, one often sees agents zigzag. This has an effect on the space occupied by a single person and therefore does not accurately represent the flow on stairs.
In crowd:it, fixed staircases, escalators and elevators can be modelled directly, giving more realistic results.
Individual Layer
The individual or behavioural layer describes the cognition and characteristics of each person, such as space requirements, desired speed, mobility, knowledge of a place and individual plans. Places that are visited can be represented as points of interest.
Individual layer in crowd:it:
- Each agent has an individual plan and personal characteristics.
- By applying pre-selected heuristics, the agents interact individually with space and events. This could mean taking the shortest or fastest route across a building; or seeking the area with the most available space, or the queue with the shortest waiting time. This brings flexibility to your simulation–model the relevant simulation with the appropriate heuristic.
How can you create individual plans in crowd:it?
crowd:it agents use a list of Points of Interest (PoIs). As soon as an agent reaches a PoI and completes her task there (e.g. used the stairs or waited a while), she can consider the next PoI. Heuristics determine the order in which the PoIs are selected. This simple and flexible architecture allows you to model many use cases in a personalised manner.
Furthermore, the architecture allows us to model other factors, such as an agent’s knowledge of the location by assigning the heuristic "fastest way" for knowledgeable agents and "shortest way" for ignorant agents.
Which properties do agents have and which ones can I adjust?
crowd:it agents are automatically assigned default values for basic parameters like walking speed, size or space requirements. These are derived from studies (e.g. (12)) that form the basis of our pedestrian flow analyses (see literature list below). These standard values have been sufficiently validated (cf. (11), (17)). However, if you have a specific population that deviates from these standard values, such as a school of children, these values can be adjusted.
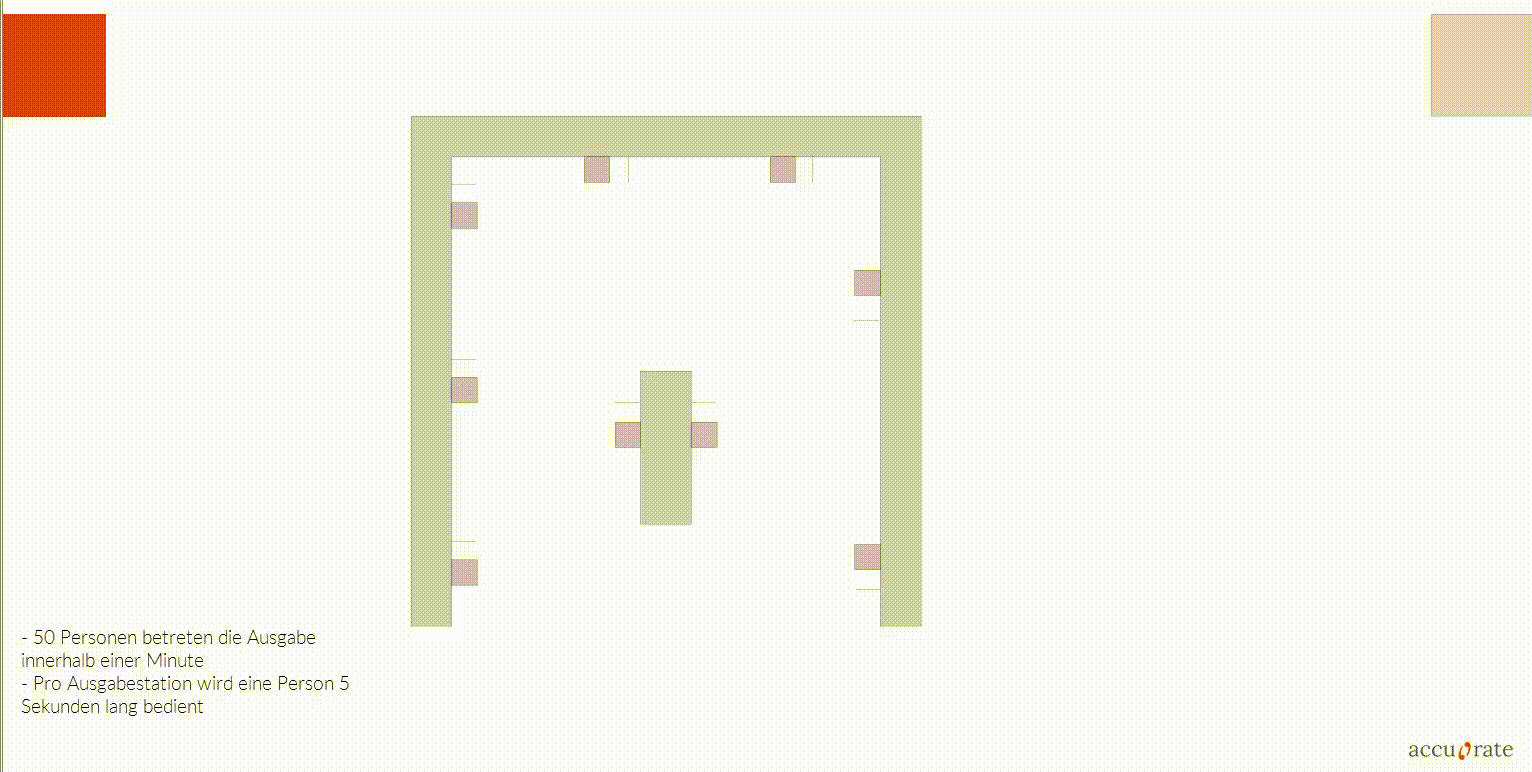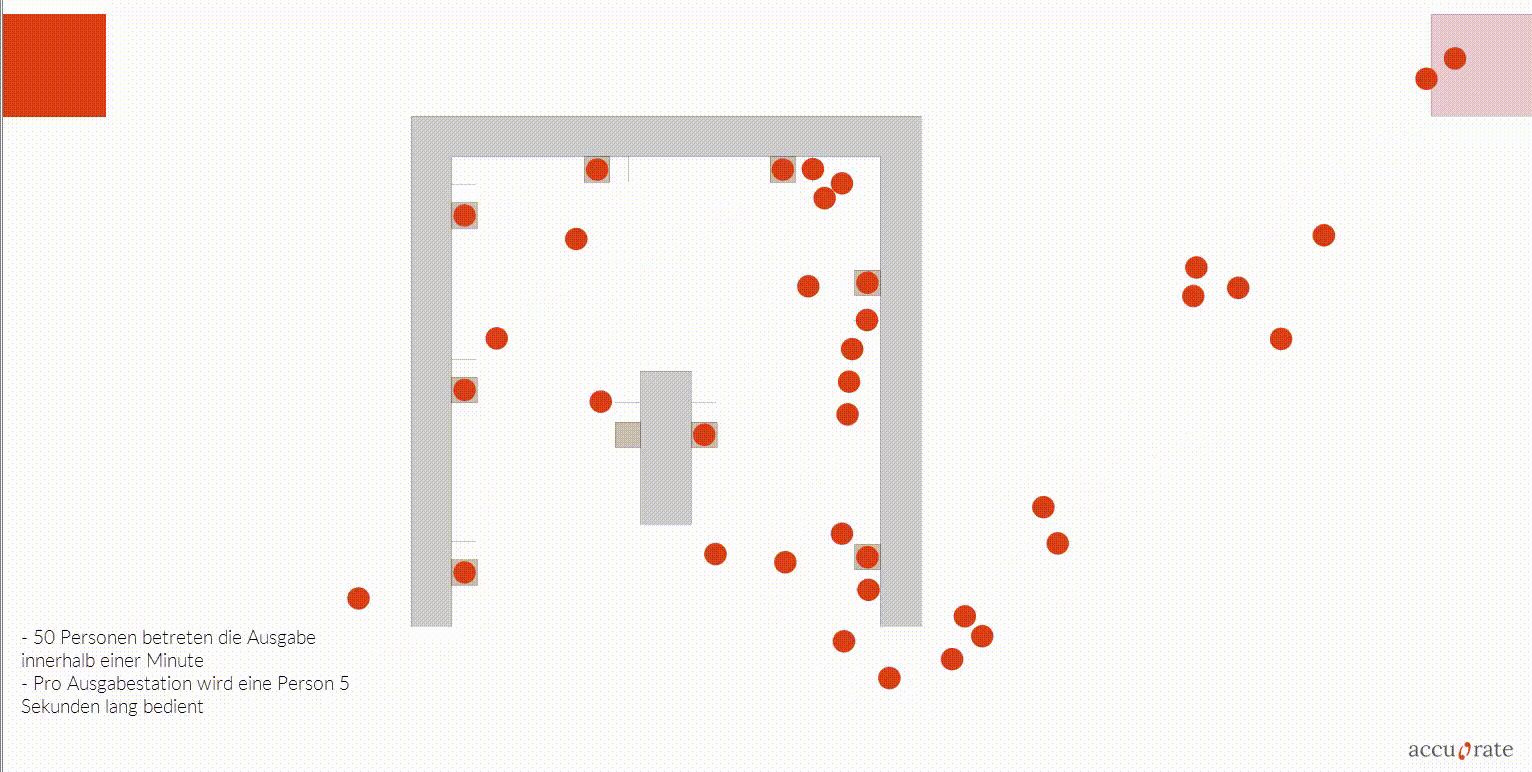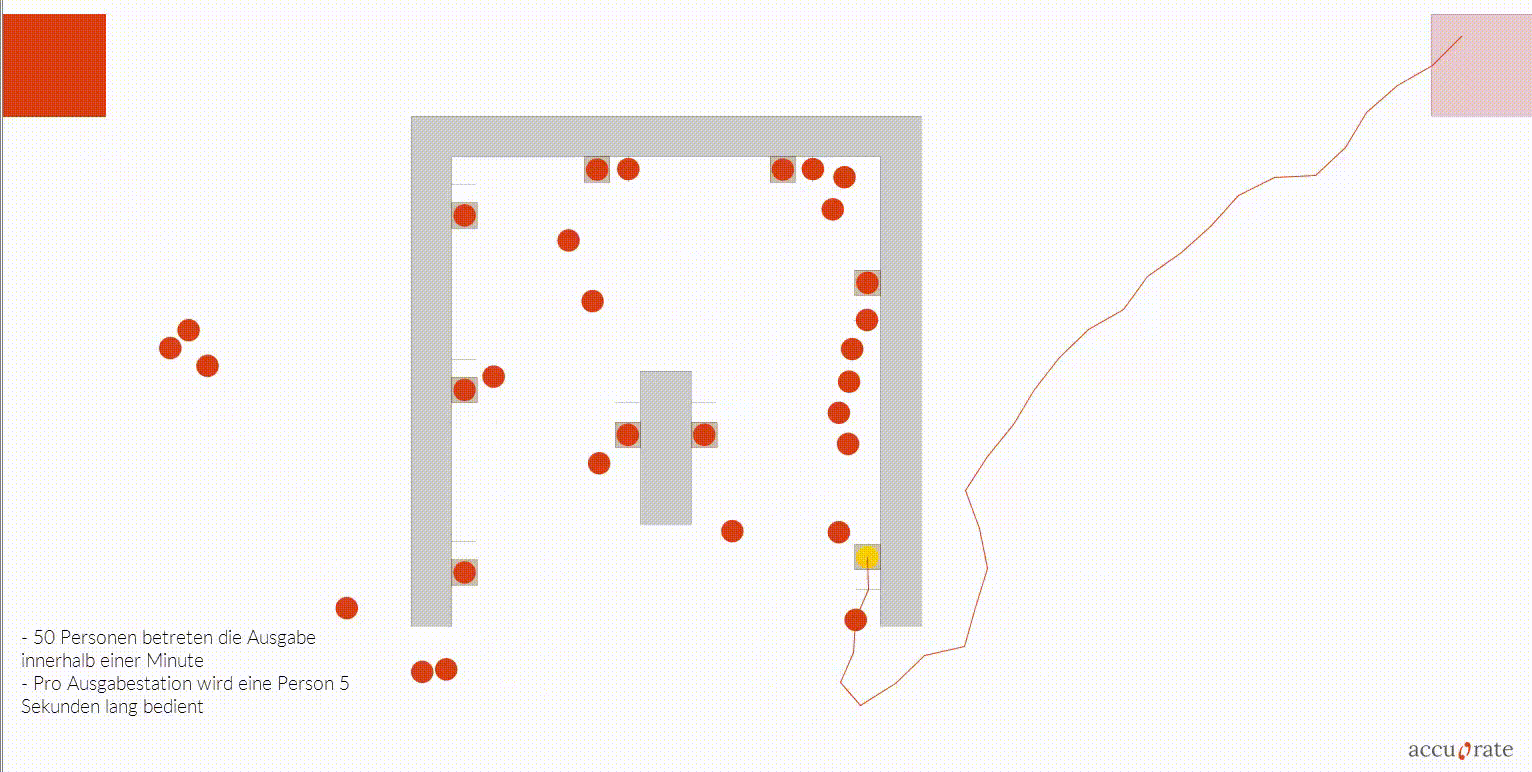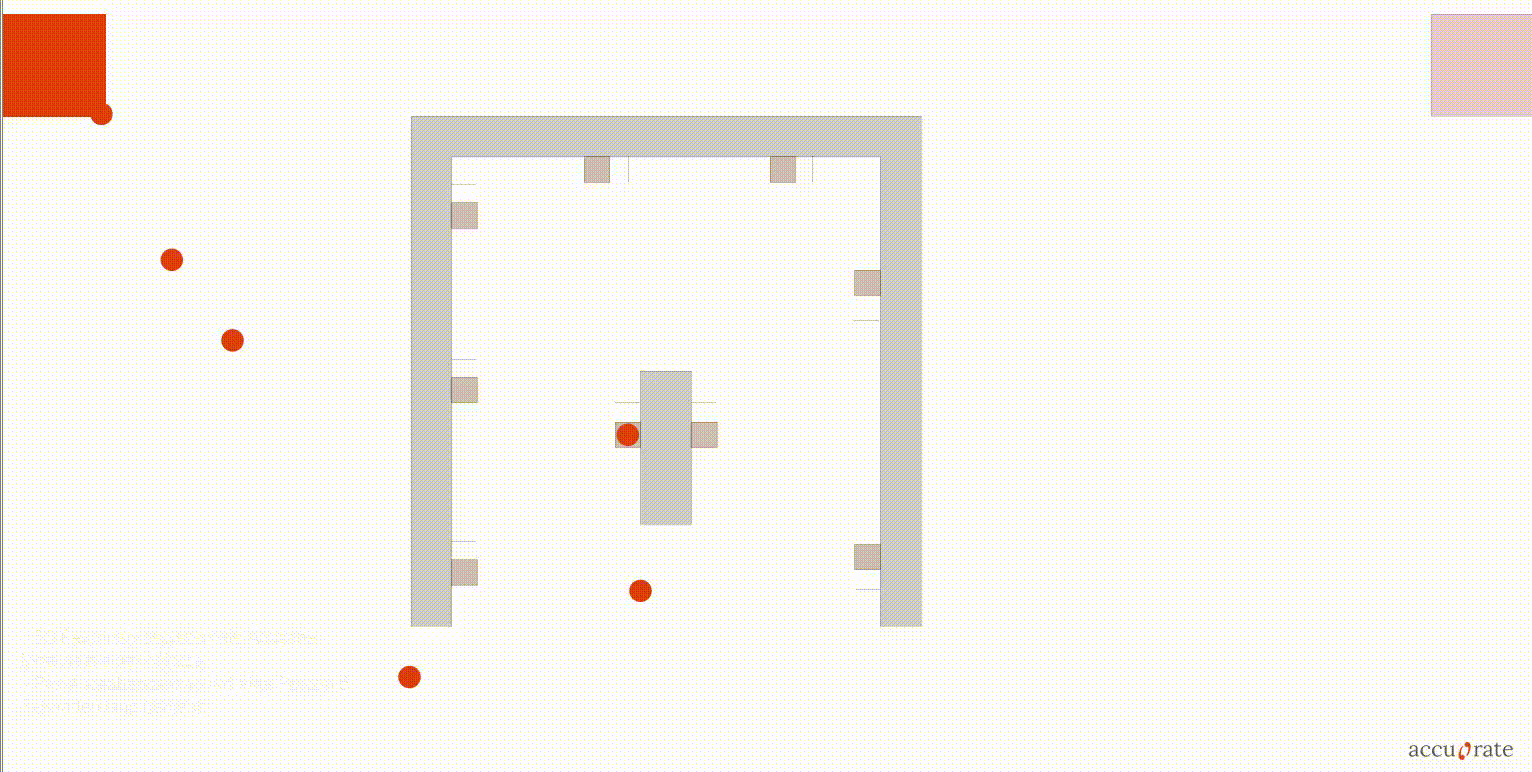
Interaction Layer
The interaction layer models social and environment interactions. This includes: queuing, waiting areas, group behaviour. In addition, the interaction layer can enforce site-specific conditions such as timetables and safety-relevant processes.
- Any number of agents, routes and characteristics can be combined.
- Our agents reflect real human behaviour, avoid collisions and obstacles and look for the easiest way to their destination. Overcrowding, lane formation and inefficient pedestrian guidance are thus realistically represented.
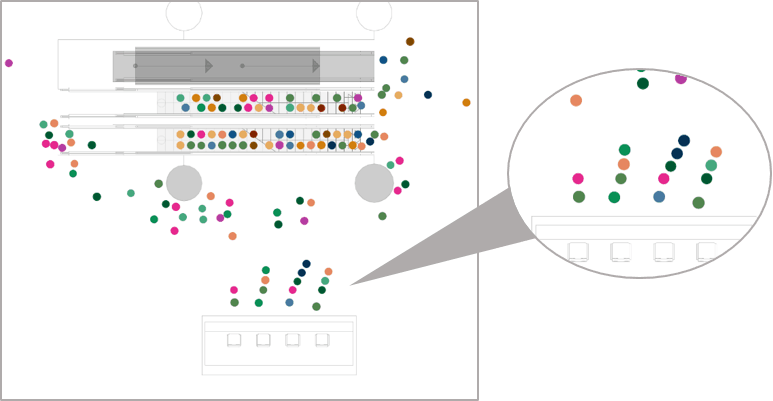
Computational Modeling
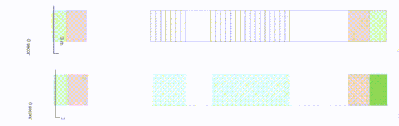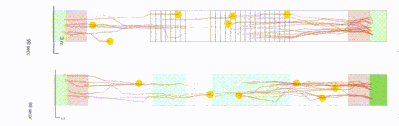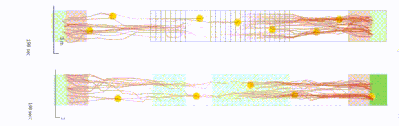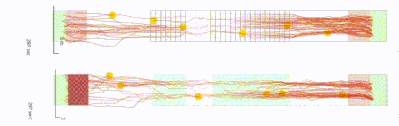
In the field of pedestrian simulation, two aspects are particularly important: How do I move in space and when do I move, i.e. spatial and temporal decisions. Here we distinguish between a discrete up to a quasi-continuous mapping:
Why quasi-continuous? Since each computer can calculate only discretely (each calculation is executed in the clock of the processor) a temporal discretization takes place inevitably for each computer program of the world. The same is true for the spatial discretization: The continuity existing in reality can only be approximated by the computers.
However, the degree of resolution varies. While some models resolve the geometry cell-based to agent size, i.e. are still quite coarse, there are other models (such as crowd:it) whose standard resolution is quasi-continuous by interpolating support points 10cm away. The setting of the grid points can be adjusted individually and increased simply by clicking.
For the mapping of the temporal decision there are also different accuracies. Either the model assigns all agents a fixed time in which each is allowed to take a step (usually several times per second) or an agent can decide to leave at any time. The former case is implemented in models based on differential equations. These equations are then re-evaluated at each time point (e.g., social force models). We have now changed this decision from synchronized time steps to individual time steps. Because this is how reality works: people decide when to take a step without a globally ticking clock. In this way, we manage to represent human behavior even better and to get more reality into the simulation. Our software can transfer another aspect from reality into the model world.